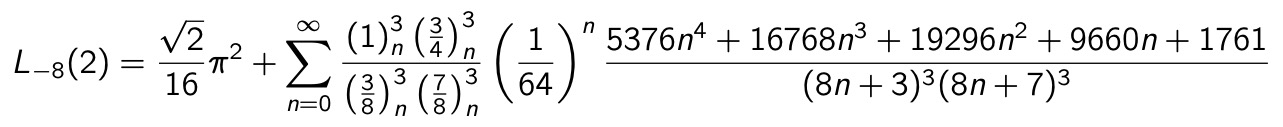Here is the fastest of my proved formulas for π (3 digits per term). I proved it by the WZ (Wilf and Zeilberger) method:
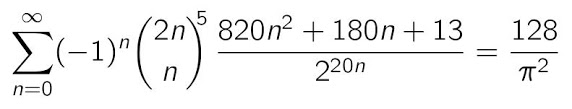
And here is the fastest of all my formulas for π (5 digits per term). It has not been proved yet. I found it using the PSLQ algorithm:
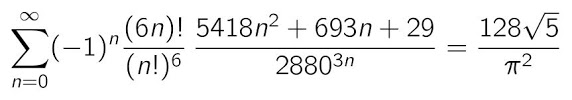
I proved an infinite product for the number e which is similar to formulas found before by Jonathan Sondow for the constants eγ and π (the exponents we see inside the parentheses are given by the rows of Pascal's triangle):
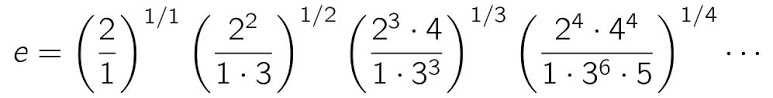
I obtained a new formula for the Catalan constant (see arXiv 1104.0396 subsection: Identity 3). It is one of the most efficient formulas for computing it (see numberworld). It reads
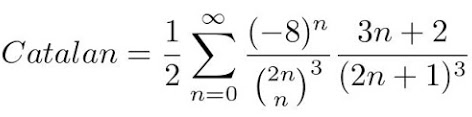
The following conjectured formula is joint with Gert Almkvist. It is interesting to observe that in the denominators there are only powers of 10 because (6n)! is divisible by (n!)6. But it is not a BBP (Bailey-Borwein-Plouffe) base 10 formula because it involves factorial numbers:
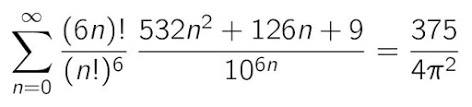
In 2013 I have obtained a new representation of the Mangoldt's function as a sum over ALL the non-trivial zeros of the Riemann zeta function. Hence, it is different from that given by Landau. In 2017 we obtained bounds. Below, we show the neat graphic that we get taking the first 10000 non-trivial zeros of zeta:
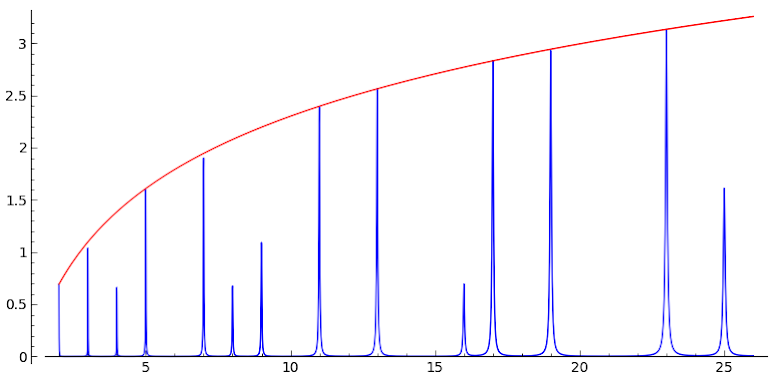
The following two fast formulas can be proved with the method explained in the paper, joint with Mathew Rogers, “Ramanujan series upside-down” (2014), and also with the method explained in my paper “Ramanujan series with a shift” (2018). The value at 2 corresponding to the character -4 (sub-index) is the Catalan constant:
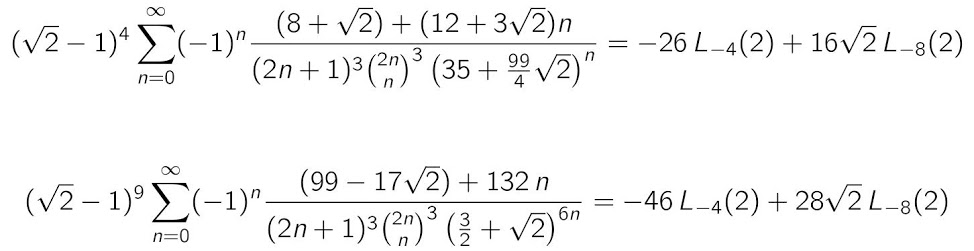
A formula for the Dirichlet value L(-7,2):
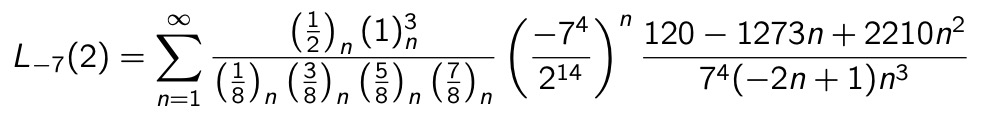
This year I have proved a new kind of algorithm generalizing those of Borwein for π. Below is a quartic algorithm depending on a free parameter w. The case w=1 is a Borwein quartic algorithm for π:
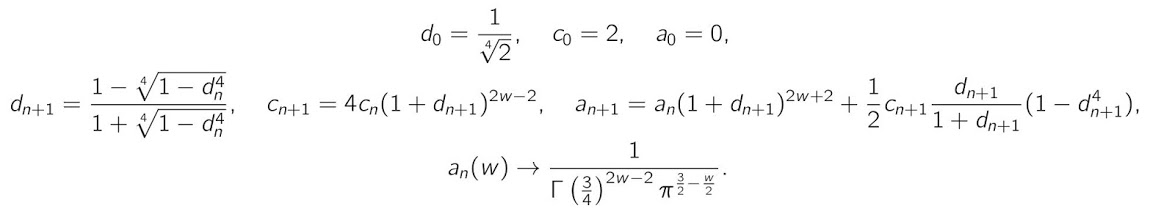
I found a new method for proving Ramanujan series for 1/π. The method is specially interesting in case of alternating series because the modular equation required in this cases has a much lower degree than that used in the other known methods. For example, the formula below was discovered by Chan, Liaw and Tan in 2000, and they knew that it could be proved using a modular equation of degree 89, but no modular equations of such degree were known (and they are still unknown today). However, in 2018 I could prove the formula using a modular equation of degree 23, that had been curiously deduced in 2000 by Chan and Liaw. I refer to this Ramanujan series as 3A23 (3=level, A=alternating, 23=degree)
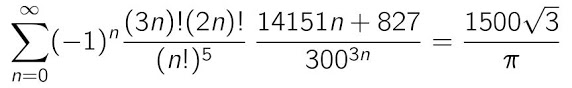
The formula below is a q-analogue of the Ramanujan series 1A3 (1=level, A=alternating, 3=degree), that we get letting q tend to 1. It was used by Wadim Zudilin for obtaining the very interesting p-adic supercongruences module p3 for the Ramanujan series 1A3
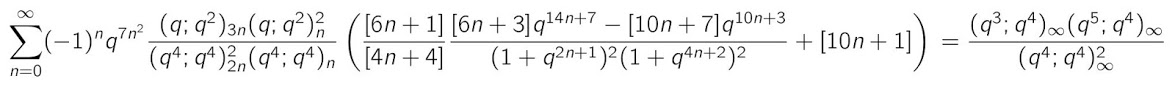
I conjectured a new kind of supercongruences related to Ramanujan-like series for π-m. Below I show an example:
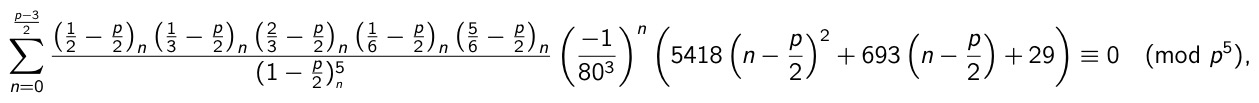
A fast formula for ω (the lemniscate constant):
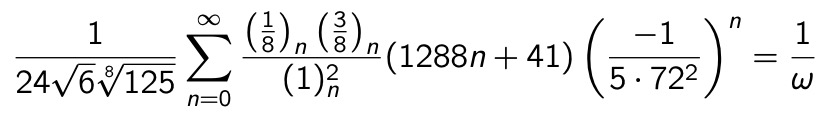
A formula for the Dirichlet value L(-3,2):
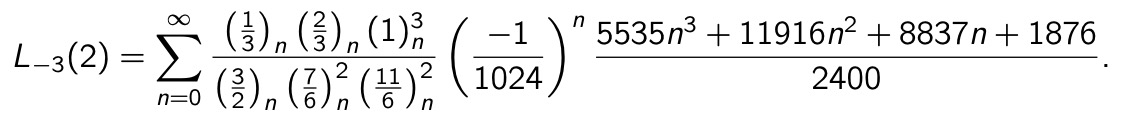
I conjectured that the coefficient of x2m+1 of the rational Ramanujan-like series for π-m of character χ extended with x is a rational multiple of L(χ, m+1). Note: If z0<0 then we replace z0n+x with (-1)n (-z0)n+x. We show an example: if we develop the series
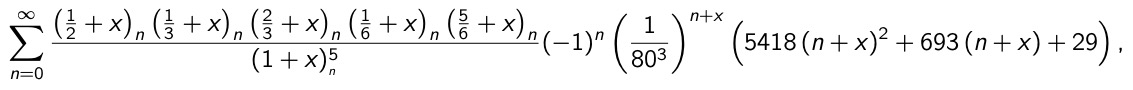
In 2023 Kam Cheong Au gave a proof of the Ramanujan-like series for 1/π3 conjectured by Boris Gourevitch. Modifying suitably the pair to avoid some problematic obstacles, and with the help of Carlson's theorem, we have obtained a beautiful generalization (WZ provable) of the Gourevitch formula (which is the specialization k=0):
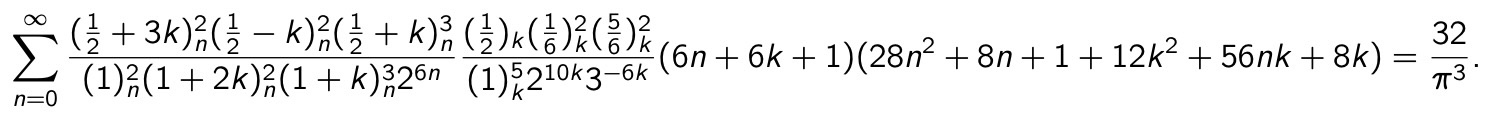
Records set by y-cruncher this year for ω (the lemniscate constant), and for the Dirichlet values L(-3,2), L(-7, 2) and L(-8,2), using my fastest formulas for their computations.
A fast computing formula for the Dirichlet value L(-8, 2):